As we’ve established, reconfiguration is a hard problem. Even for a few modules, it’s infeasible to go through the space of all possible configurations and find the optimal path from one configuration to another. Adding heuristics can help a bit, but they don’t make the problem much easier.
Recall the definiton of the reconfiguration problem: given an initial configuration A and a target configuration B, find a sequence of atomic actions (reconfiguration plan) the modules can take in order for the robot to transform from A to B. The problem itself has been proven to be NP-hard.
As with all the other NP-hard problems, we have a choice to make when trying to solve them: we either have to sacrifice speed of computation, optimality of the result, or reliability. In this section, we will introduce an algorithm that performs significantly better than graph search, at the cost of potentially making the reconfiguration plan much longer.
Intermediate Shape
Given two configurations, i.e. X and Y, let us denote knowing the sequence for reconfiguration from X to Y as X -> Y.
One key observation to making a reconfiguration plan more efficient is that given our initial shape A, target shape B, and any shape C, it holds that A -> C & C -> B implies A -> B by notion of simply appending the two reconfiguration plans. This observation may seem trivial, but if we can find a shape it’s particularly easy to reconfigure into, we’ve made the reconfiguration problem a lot easier. In addition, we can assume that C -> B implies B -> C, as we can – aside from possible outside forces like gravity – reverse the reconfiguration steps.
How does that help us? One shape that is particularly simple into is a snake configuration. Such a configuration consists of uniform modules connected in a row via the same connector, and is therefore uniquely defined by the number of modules.

The algorithm for finding a reconfiguration plan then looks as follows:
-
Find reconfiguration plan from A to snake
-
Find reconfiguration plan from B to snake
-
Reverse the found reconfiguration plan from B to snake
-
Append the plans to get a reconfiguration plan from A to B
Reconfiguration to Snake
When trying to come up with an efficient algorithm for reconfiguring any configuration to a snake, it’s helpful to look away from the physical shape, and instead view the inner structure of the robot as a graph. In this graph, each vertex can represent a module. Each vertex has at most 6 neighbors, and the edges specify the type of connection between the modules. In this definition, a snake can be defined as follows: the graph is connected, each vertex has at most two neighbors, and all the inter-module edges are of the same type.
The first step in transforming any graph of RoFI modules to a snake is transforming it into a tree. To achieve that, we remove any cycles from the tree by removing redundant connections between modules. A straightforward way of realizing the removal of cycles is to traverse the inner structure via DFS and remove any edges that lead to modules that have already been found.
Once the inner structure is a tree, we can start the transformation to a snake by removing redundant branches. The procedure is quite simple: take two branches, connect them, cut one of them off at the base. With the right choice of which branches to connect and where to cut, repeating this procedure converges to a snake configuration.
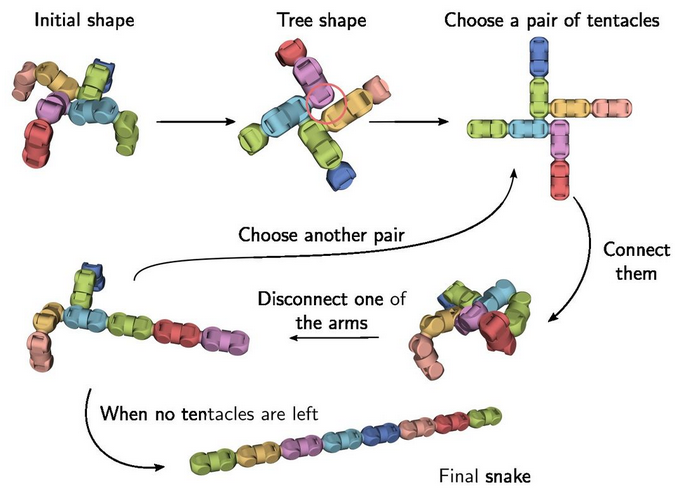
Connecting the Branches
The question that still needs answering is how to perform the branch connection. We’ve discussed how to reach a target with an arm consisting of multiple modules here, but in this case, there isn’t a single target; we don’t know where the best place for the branches to connect is.
Fortunately, we can solve the problem via a reduction to the single target problem. To start, the algorithm simulates a single arm by virtually connecting the two branches and disconnecting one at the base. Once we have an extended arm, we can set the disconnected arm’s base as the new target, and reach it with any method for controlling robotic arms.
If a solution is found, we’ve computed positions where the two branches can connect, and the actual movement is realised. If a solution is not found, a different pair of branches is tested out instead, potentially backtracking to previous arm connections.

And with that, the algorithm is complete. It’s fast and elegant, but it does come with its drawbacks. Regardless of how close the initial and target configurations are, the algorithm always proceeds all the way to snake. This is far from optimal, and impractical for robots operating in an enclosed space. Ideally, we would like to shorten the resulting reconfiguration plan by finding different intermediate shapes, such as common subtrees of the initial and target configurations.
